Publications and Preprints
Markus SchmidmeierFlorida Atlantic University
Mathematical Reviews arXiv ORCID
-
X. Luo, M. Schmidmeier, Gorenstein-projective modules over the ring of dual integers, (2025), 18 pp., arXiv.
-
X. Luo, M. Schmidmeier, A reflection equivalence for Gorenstein-projective quiver representations, (2022), 35 pp., arXiv.
-
J. Kosakowska, M. Schmidmeier, M. Schreiner, Abelian p-groups with a fixed elementary subgroup or with a fixed elementary quotient, Arch. Math. 125, 235-246 (2025), DOI, arXiv.
-
C. M. Ringel, M. Schmidmeier, Invariant subspaces of nilpotent operators. Level, mean and colevel: The triangle 𝕋(n), Bulletin of the Iranian Mathematical Society (2025) 51:37, 179 pp., 157 illustrations, DOI, arXiv.
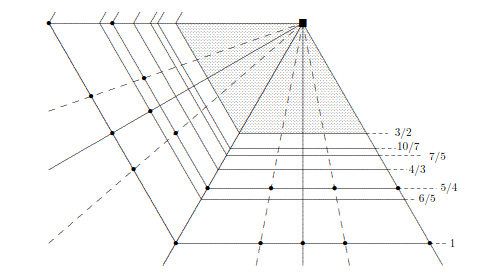
At BIMS, our paper is Invited Paper #12. -
M. Schmidmeier, Hammocks to visualize the support of a finitely presented functor, J. Algebra 616 (2023), 68-96, DOI, arXiv.
-
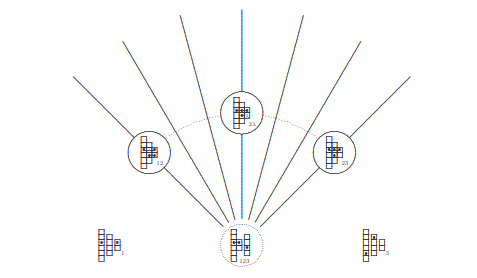
J. Kosakowska, M. Schmidmeier, The socle tableau as a dual version of the Littlewood-Richardson tableau, dedicated to Andrzej Skowroński, J. London Math. Soc (2) 106 (2022), 1357-1379, DOI, arXiv.
-
J. Kosakowska, M. Schmidmeier, Finite direct sums of cyclic embeddings, in: Advances in representation theory of algebras (Proc. Conf. on the occasion of the 60th birthday of Professor José Antonio de la Peña), Contemp. Math. 761, Amer. Math. Soc., Providence, RI, (2021), DOI, arXiv.
-
J. Kosakowska, M. Schmidmeier, and H. R. Thomas, Two Partial Orders for Standard Young Tableaux, The Electronic Journal of Combinatorics, 26 (3), #P3.20 (2019), 18 pp., DOI, journal, arXiv.
-
M. Schmidmeier, From Schritte and Wechsel to Coxeter groups, In: Mathematics and Computation in Music. MCM 2019. Lecture Notes in Computer Science, 11502 (2019), 113-124, Springer, DOI, arXiv.
-
M. Schmidmeier, 2:3:4-Harmony within the Tritave, Journal of Mathematics and Music 13 (2019), 222-244, DOI, arXiv.
-
P. Dowbor, H. Meltzer, M. Schmidmeier, The "0,1-Property" of Exceptional Objects for Nilpotent Operators of Degree 6 with One Invariant Subspace, J. Pure Appl. Alg. 223 (2019), 3150-3203, DOI.
-
J. Kosakowska and M. Schmidmeier, The Boundary of the Irreducible Components for Invariant Subspace Varieties; Mathematische Zeitschrift 290 (2018), 953-972, DOI (free access), arXiv.
-
M. Kaniecki, J. Kosakowska and M. Schmidmeier, Operations on arc diagrams and degenerations for invariant subspaces of linear operators. Part II, Communications in Algebra 46:5 (2017), 2243-2263 Free e-link, DOI, arXiv.
-
J. Kosakowska and M. Schmidmeier, Box moves on Littlewood-Richardson tableaux and an application to invariant subspace varieties, dedicated to Fred Richman, J. Algebra 491, 241-264 (2017), DOI, arXiv.
-
A. Moore and M. Schmidmeier, The Swiss Cheese Theorem for Linear Operators with Two Invariant Subspaces, Proc. Amer. Math. Soc. 143 (2015), 5097-5111, DOI, arXiv.
-
J. Kosakowska and M. Schmidmeier, Operations on Arc Diagrams and Degenerations for Invariant Subspaces of Linear Operators; dedicated to Daniel Simson, Trans. Amer. Math. Soc. 367 (2015), 5475-5505, DOI, article, arXiv.
-
J. Kosakowska and M. Schmidmeier, Arc Diagram Varieties; in: "Expository lectures on representation theory", Contemporary Mathematics 607, Amer. Math. Soc., Providence, RI, (2014), 205--224, arXiv, DOI.
-
M. Schmidmeier and H. Tyler, The Auslander-Reiten Components in the Rhombic Picture; dedicated to Mark Kleiner on the occasion of his 65th birthday, Comm. Alg. 42 (2014) 1312-1336, DOI, article, arXiv.
-
M. Schmidmeier, Hall polynomials via automorphisms of short exact sequences; dedicated to Wolfgang Zimmermann, Algebras and Representation Theory 15 (2012), 449-481, DOI, article, arXiv.
-
M. Schmidmeier, The entries in the LR-tableau; Mathematische Zeitschrift 268 (2011), 211-222, DOI, article, arXiv.
-
C. Petroro and M. Schmidmeier, Abelian groups with a p2-bounded subgroup, revisited; Journal of Algebra and its Applications 10 (2011), 377-389, DOI, arXiv, article.
-
G. Marks and M. Schmidmeier, Extensions of simple modules and the converse of Schur's Lemma; in: Advances in Ring Theory, Trends in Mathematics, 229-237, Birkhäuser Verlag Basel/Switzerland (2010), DOI, article, arXiv.
-
H.-D. Gronau and M. Schmidmeier, Orthogonal covers by multiplication graphs, Discrete Appl. Math. 157 (2009), 2048-2056, DOI.
-
M. Schmidmeier, Systems of submodules and an isomorphism problem for Auslander-Reiten quivers, Bull. Belg. Math. Soc. Simon Stevin 15 (2008), 523-546, article, arXiv.
-
C. M. Ringel and M. Schmidmeier, Invariant Subspaces of Nilpotent Linear Operators. I., Journal für die reine und angewandte Mathematik 614 (2008), 1-52, DOI, Crelle, arXiv.
-
C. M. Ringel and M. Schmidmeier, The Auslander-Reiten Translation in Submodule Categories, dedicated to Idun Reiten, Trans. Amer. Math. Soc. 360 (2008), 691-716, DOI, arXiv.
-
C. M. Ringel and M. Schmidmeier, Submodule categories of wild representation type, Journal of Pure and Applied Algebra 205/2 (2006), 412-422; DOI, Science Direct; arXiv.
-
M. Schmidmeier, Bounded Submodules of Modules, dedicated to Claus Michael Ringel on the occasion of his 60th birthday, Journal of Pure and Applied Algebra 203 (2005), 45-82, DOI, arXiv.
-
M. Schmidmeier, A Construction of Metabelian Groups, Archiv der Mathematik 84 (2005), 392-397; DOI, arXiv.
-
M. Schmidmeier, A family of noetherian rings with their finite length modules under control, dedicated to Helmut Lenzing on the occasion of his 60th birthday, Czechoslovak Mathematical Journal 52 (3), (2002), 545--552, DOI.
-
M. Schmidmeier, Ring Units in iterated cyclic extensions, and in NTRU, Tatra Mountains Mathematical Publications 25 (2002), 127-136, PDF.
-
M. Schmidmeier, When are artinian PI-rings artin algebras?, Comm. Alg., 29 (4), (2001), 1659-1668, DOI.
-
M. Schmidmeier, The finite length modules for thin Z-graded rings, Comm. Alg., 29 (3) (2001), 1041--1067, DOI.
-
M. Schmidmeier, Endofinite modules over hereditary artinian PI-rings, Proc. Conf. ICRA VIII, Canadian Mathematical Society Conference Proceedings 24 (1998), 497 - 511, PDF.
-
M. Schmidmeier, The local duality for homomorphisms and an application to pure semisimple PI-rings, Colloquium Mathematicum 77 (1998), 121 - 132, journal article.
-
M. Schmidmeier, Auslander-Reiten theory for artinian PI-rings, J. Alg. 207 (1998), 72--81, DOI.
-
M. Schmidmeier, A dichotomy for finite length modules induced by the local duality, Comm. Alg. 25 (1997), 1933--1944, DOI.
-
M. Schmidmeier, Auslander-Reiten-Köcher für artinsche Ringe mit Polynomidentität, Ph. D. Dissertation, Universität München, 1996, PDF.
"This article could be used for pedagogical purposes in a course on tiling groups, Coxeter groups, quotient groups, etc."

Last modified: by Markus Schmidmeier